Multiphysics Simulation of Smart Devices

Martensitic Phase Change Model

The martensitic phase change is described by a phenomenological model, which has been extended to structures of arbitrary 3D shape and implemented in the COMSOL Multiphysics software package. For engineering applications, a continuum model is most suitable, since it makes use of measureable quantities as parameters. Each material point is considered as a two-phase mixture, where each phase is described by one or more internal variables. The kinetic of the phase change is described by two exponential functions, one for the forward transformation from the high temperature austenite to the low-temperature martensite phase and one for the reverse transformation. Both of them depend on the actual temperature and the stress. For instance, the transformation from martensitic to the austenitic phase is described by equation (1).

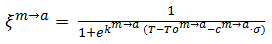(1)

Besides the temperature T and the mechanical stress σ, the following parameters determine the transformation: The transition temperature To, the stress rate c and the width of the transition k. This simple model not only allows to have an insight in the phase distribution in the device, but also to link the material properties of the shape memory alloy to its actual phase.

For example, the electrical resistance is described by combining the resistances of martensite and austenite according to the rule of mixture:

(2)

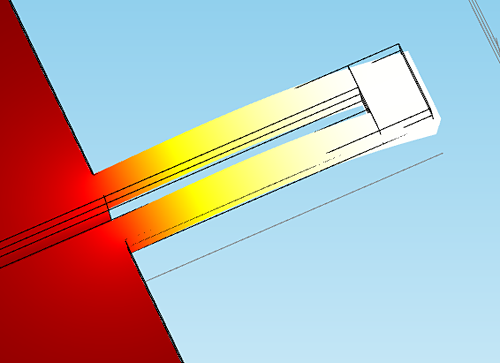
This allows to model temperature profiles originating from Joule heating. The Young’s Moduli are implemented in an analogous way to simulate the mechanical behavior, e.g., the deformation of an SMA-Si-bimorph. Thus, first approximations on the behavior of a SMA device are possible, see Fig. 1.

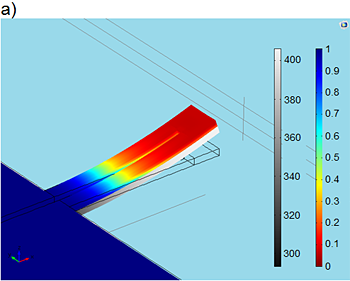
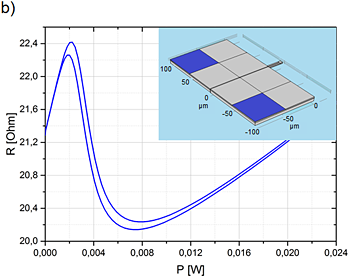
Figure 2: Simulation results for a SMA/Si-bimorph double-beam cantilever during phase transformation. (a) The grey color scale in the Si layer shows the temperature gradient along the double beam, whereas the color code used for the SMA layer indicates the profile of martensitic phase. The value of “0” indicates zero martensite and, thus, 100% austenite. (b) Electrical resistance versus applied power. The electrical contact pads are indicated in the inset in blue.

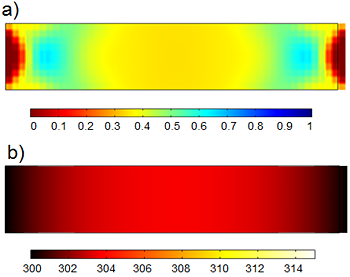
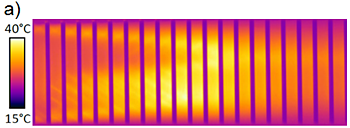
Another field of application is the use of the pseudoelastic effect that is caused by stress-induced phase transformation in contrast to the thermally induced shape memory effect. During phase transformation in shape memory alloys, a relatively large amount of latent heat is released or absorbed depending on the direction of phase transformation. This elastocaloric effect is of large interest for applications in small dimensions. In order to implement this property in our simulation model, a phase-change dependent heat capacity is taken into account. Thus, it is possible to simulate the temperature distribution caused by a stress-induced phase transition as shown in Fig. 2 for a pseudoelastic SMA stripe sample.

Figure 2: Simulation results for a pseudoelastic SMA stripe during stress-induced phase transformation. (a) Profile of martensitic phase, (b) corresponding temperature profile. The phase transformation is simulated for loading and unloading. The corresponding stress-strain characteristics are shown in (c) for various strain rates.

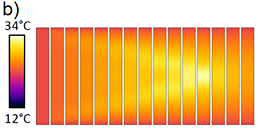
Figure 3 shows experimental and simulated temperature profiles. In the experiment, heating is observed to be inhomogeneous. Areas with elevated temperature arise starting from the region of sample fixation and propagating towards the sample center. This phenomenon is also described by our simulation model, see [1] for more details.

Figure 3: Temperature profiles in a SMA stripe sample observed after certain time intervals during a load cycle, a) experiment, b) simulation.

Magnetic Reorientation Model

In addition to thermally induced deformation, single crystalline ferromagnetic shape memory alloys such as Ni-Mn-Ga exhibit large deformations of up to 12% by applying an external magnetic field. This magnetic shape memory effect is based on a field-induced reorientation of martensite variants. The magnetic shape memory effect is used in MSM microactuators for switching and positioning applications.

The thermodynamic model for field-induced reorientation relies on the formulation of Gibbs free energy as a sum of mechanical and magnetic contributions

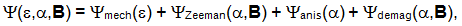(3)

where Zeeman energy, magnetocrystalline anisotropy energy and magnetostatic energy are considered here depending on magnetization and magnetic induction B [2-4]. For the mechanical contribution, only the linear strain e is extracted from the 3D strain tensor in the simulation to map the energy path during reorientation, see Fig. 4. The internal variable magnetization is defined via the magnitude of the applied field, the saturation magnetization and the local inclination angle α with respect to the magnetic easy axis. The resulting energy landscape is given in Fig. 5. This shows different minima depending on the external load that constitute the stability regions of the system. Reorientation is assumed to be a thermally activated process in the model allowing the use of rate equations to describe the volume fractions of each martensite variant (as well as for austenite depending on temperature).

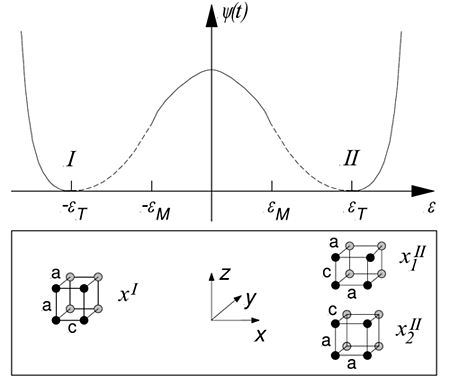Figure 4: Mechanical contribution of free energy (at zero external stress) of the crystallographic variants I and II in Ni-Mn-Ga (10 M martensite). The crystal structure (schematic) shows the shorter c axis and two longer a axes.

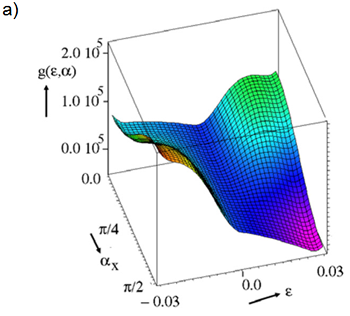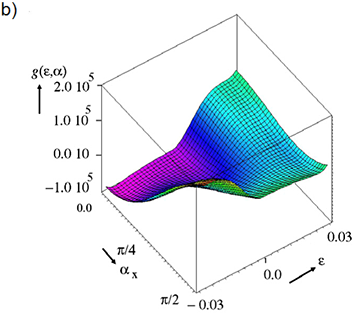Figure 5: Energy landscape of Ni-Mn-Ga as a function of strain ε and inclination angle of the magnetization α with respect to the x axis. At an external tensile load of 1.5 MPa and zero magnetic field, the energy minimum is in the extended state (ε=0.03) (a), whereas at zero external load and a magnetic field of 0.2 T, the shortened state (ε=-0.03) has the lowest energy [5].

By finite element modeling, the coupled magnetic, mechanical and kinetic processes of phase transformation are described in space and time, and are solved self-consistently by an iterative algorithm. Simulation results are depicted in Fig. 6(a) for a foil actuator that is prestressed by a tensile spring. Due to the simple linear deformation, discretization is possible by using only a few elements that describe mechanically active and inactive regions. The characteristics of strain versus magnetic field are nonlinear and strongly depend on the prestress generated by the spring. In the case of too low prestress (< 1.5 MPa), only partial resetting occurs. Completely reversible actuation cycles occur above the prestress of 1.5 MPa. For further increasing prestress (> 1.5 MPa), the maximum deformation decreases, because the magnetic shape memory effect becomes incomplete. Above the blocking stress (about 3 MPa), martensite variants can no longer be reoriented by a magnetic field. The simulation model qualitatively describes the experimentally observed behavior.

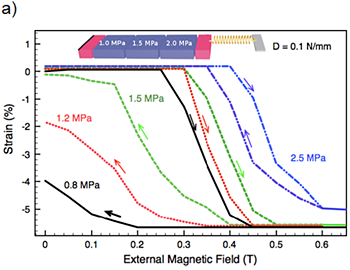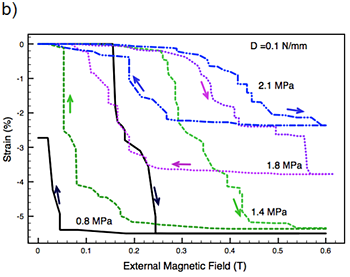Figure 6: Strain characteristics as a function of external magnetic field of a MSM linear actuator of NiMnGa with an elastic reset spring (spring constant D=1 N/mm) for different levels of prestress generated by the spring. (a) Simulation: The heterogeneous material behavior is represented by three elements having different values of twinning stress (1- 2 MPa) that have to be overcome for reorientation of martensite variants. The simulated characteristics strongly depend on the prestress. Above a prestress of 1.5 MPa, reversible actuation cycles occur showing complete resetting. The setup of the actuator is shown schematically in the inset. (b) Experiment [6].

Further information:

1. H. Ossmer, F. Lambrecht, M. Gültig, C. Chluba, E. Quandt, M. Kohl, Evolution of temperature profiles in TiNi films for elastocaloric cooling, Acta Materialia 81, 2014, pp. 9–20 (https://www.sciencedirect.com/science/article/pii/S1359645414005977)
   [doi:10.1016/j.actamat.2014.08.006].
2. M. Kohl, M. Gueltig, V. Pinneker, R. Yin, F. Wendler, and B. Krevet, Magnetic Shape Memory Microactuators, Micromachines 5, (2014), 1135-1160.
3. B. Krevet, V. Pinneker, M. Kohl, A magnetic shape memory foil actuator loaded by a spring, Smart Mater. Struct. 21 (2012) 094013 1-7.
4. M. Kohl, B. Krevet, S. R. Yeduru, Y. Ezer and A. Sozinov, A novel foil actuator using the magnetic shape memory effect, Smart Mater. Struct. 20 (2011) 094009 1-8.